An interesting series convergence using geometry. Putnam 2021 A3.
Context
Series convergence arguments using geometry tend to be particularly beautiful. I came across this a competition problem which admits an unusual, pretty argument.
Problem
This is from Putnam 2021, problem A3.
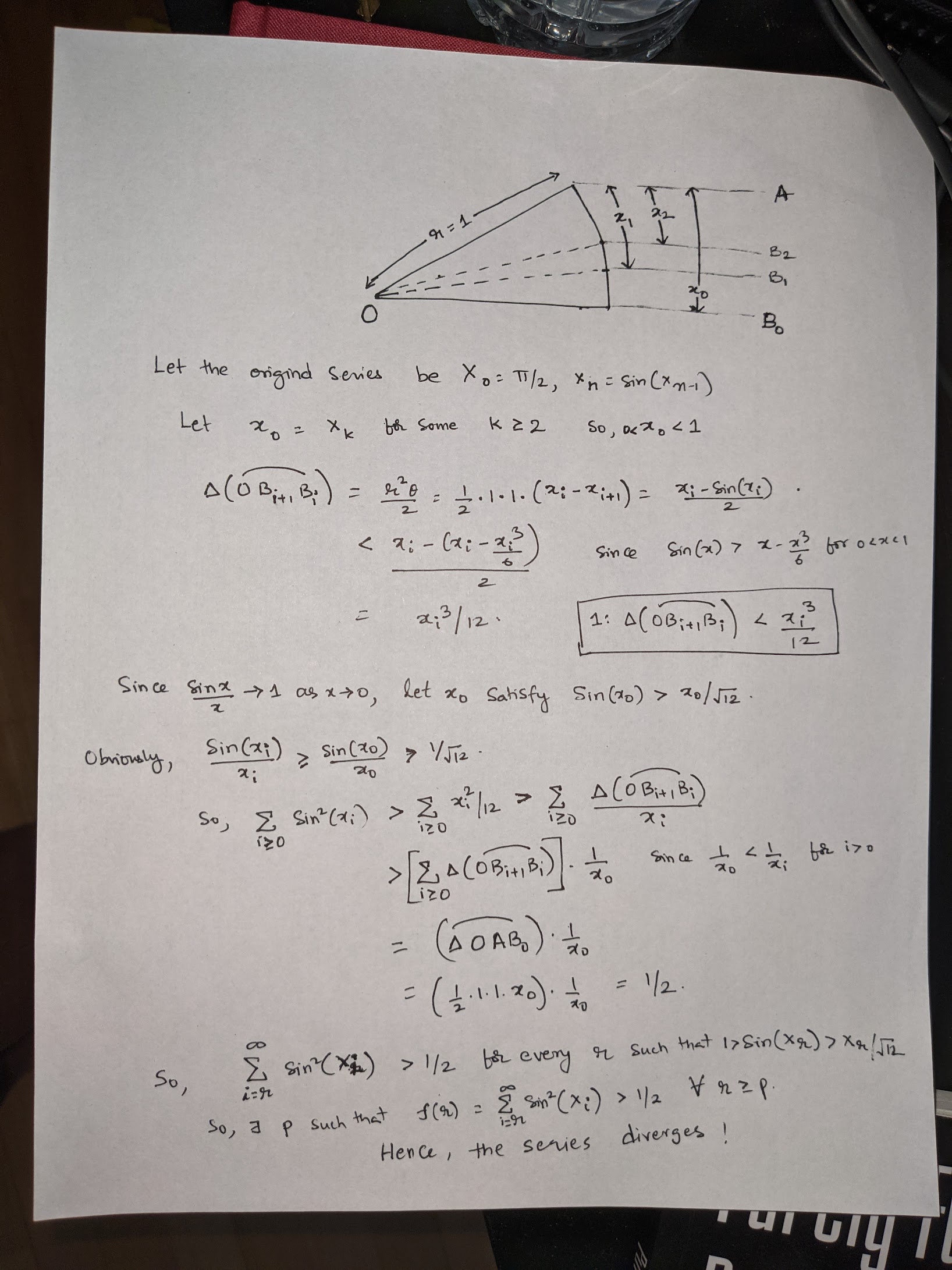
Let \(a_0 = \pi/2\) and let \(a_n = sin(a_{n-1})\) for \(n \ge 1\). Determine whether the following series converges:
\[\sum_{n=1}^\infty a_n^2\]Solution
This is my handwritten solution; it leaves out some facts without quoting them or proving them (exercise for reader!) such as:
- \(a_n\) is monotonically decreasing
- \(sin(x)/x\) monotonically increases to 1 as x decreases from \(\pi/2 \to 0\) (bounds excluded)
- \(sin(x) \gt x - x^3/6\) for \(0 \lt x \lt 1\)
- If a series \(\sum_{n=1}^\infty s_n, s_n \gt 0\) is such that \(\exists p \ge 1: \forall r \ge p, (\sum_{i=r}^\infty s_n) > k\) for some fixed \(k \gt 0\), then the series diverges
The solution converts the recursive structure in \(x_n = sin(x_{n-1})\) to a series of arc lengths on the unit circle and the series sum \(\sum_{n=1}^\infty a_n^2\) can then be compared to the arc areas.
Enjoy Reading This Article?
Here are some more articles you might like to read next: